Finding bounding boxes with interval math
Consider the implicit surface representation of a circle with radius 1:
$$ f(x, y) = \sqrt{x^2 + y^2} - 1 $$
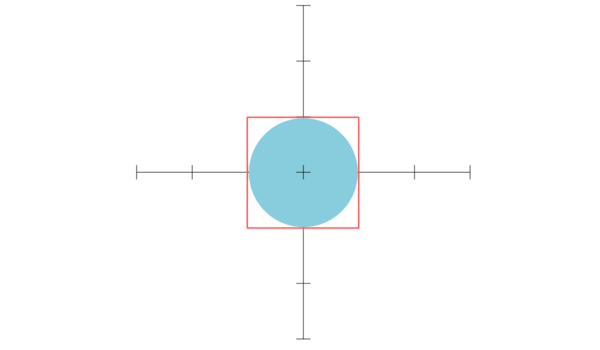
Drawn in the 2D plane, it looks like this:

Since we set its radius, we know it is bounded by $ -1 \leq x \leq 1$; $ -1 \leq y \leq 1 $.
From inside the system, though, we just have a black box that takes two arguments and returns a single value. Since we're using signed distance fields, $f$ returns a negative value inside the shape and a positive value outside.
This writeup discusses automatically finding a bounding box for an arbitrary black-box distance function, with one condition: the black box must also be callable on intervals, e.g. using the rules of interval arithmetic.
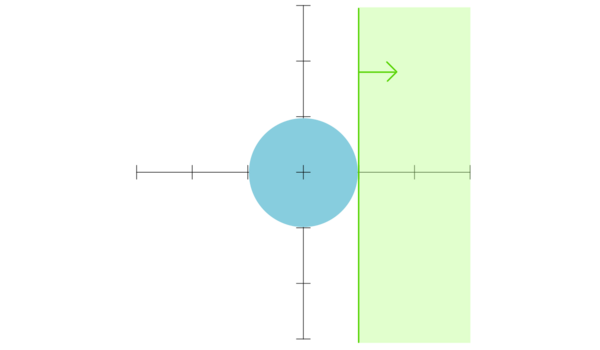
We'll start out using half-spaces. Consider the half-space with the bounds
- $X = \left[x_\text{max}, \infty\right]$
- $Y = \left[-\infty, \infty\right]$
The upper bound of $f(X, Y)$ will always be $\infty$, but the lower bound will give us valuable information:
- If the lower bound is $\leq 0$, then the shape could be within the half-space
- Otherwise, the shape cannot be within the half-space
If we minimize $x_\text{max}$ subject to $f(X, Y) > 0$, we'll have found a value for $x_\text{max}$ that definitely doesn't include the shape.
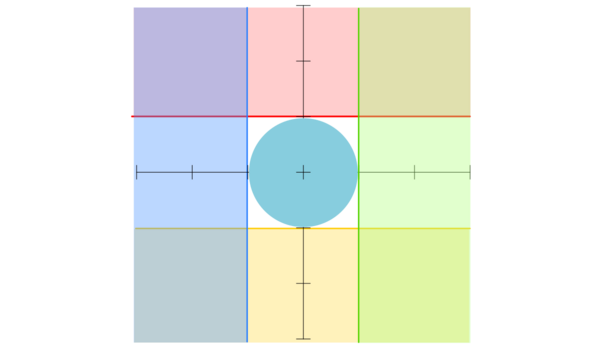
We can repeat this for three other halfspaces, and find guaranteed spaces where the shape isn't:
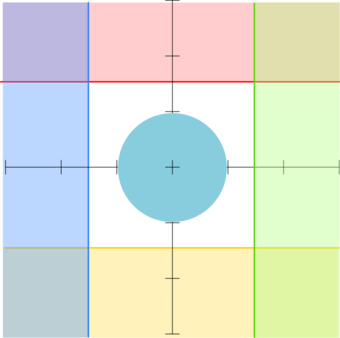
Then, just flip the spaces to build a box where the shape could be. In this case, it lines up perfectly with the original, true bounds:

That was easy!
Unfortunately, it's easy to find cases that break this strategy.
Consider rotating $f$ by 45º, by remapping $x$ and $y$ in the original equation:
$$ g(x, y) = \sqrt{\left(\frac{x - y}{\sqrt 2}\right)^2 + \left(\frac{y + x}{\sqrt 2}\right)^2} - 1 $$
If we use the same half-space
- $X = \left[x_\text{max}, \infty\right]$
- $Y = \left[-\infty, \infty\right]$
then the result is always $g(X, Y) = \left[-0.5, \infty\right]$.
(Plug in the bounds and check the interval math if this doesn't make sense)
This interval means we can never be sure that we're outside the shape, so our search will go to infinity along every axis.
We're not out of tricks yet, though.
Instead of a half-space, let's use a pair of quarter-spaces:
- $X = \left[x_\text{max}, \infty\right]$
- $Y = \left[0, \infty\right]$
and
- $X = \left[x_\text{max}, \infty\right]$
- $Y = \left[-\infty, 0\right]$
The union of these two quarter-spaces is the same half-space as before, but having only one infinity (rather than two) in the $Y$ term makes the math more forgiving.
If you do the same kind of search, you'll find the bounds for the shape are
$$ -1.414 \leq X \leq 1.414 $$ $$ -1.414 \leq Y \leq 1.414 $$
This isn't as tight as possible, but it's not too bad:
(Did you notice that the bounds grew by a factor of $\sqrt 2$ ?)
Sadly, this fix doesn't work in the general case either.
Consider the tiny transform
$$ h(x, y) = \sqrt{\left(x - 0.0001y\right)^2 + \left(y + 0.0001x\right)^2} - 1 $$
(equivalent to rotating by almost 0º)
Using the quarter-space strategy, we find that the bounds are at least
$$ -10000.125 \leq X \leq 10000.125 $$ $$ -10000.125 \leq Y \leq 10000.125 $$
While that is technically correct, it's not very useful.
This is the point where interval arithmetic starts to fail us:
Because intervals don't know that the two squared terms vary together,
the worst-case estimate is incredibly bad.
The correct answer is to switch to
affine arithmetic;
implementation is left as an exercise to the reader.