A simple adversarial model for dual contouring
In dual contouring-style meshing of implicit surfaces, 3D space is broken into a set of cells; think of them as a grid of small cubes. If the isosurface crosses through a cell, then a mesh vertex is associated with that cell.
(A more detailed explanation of dual contouring is available in this writeup)
The position of the vertex is based on Hermite data at the intersections of the cell edges and the isosurface. At each intersection, we know the position – which is somewhere on the cell edge – and the normal of the isosurface. Using the position and normal, we solve a Quadratic Error Function to find the position of the vertex.
This works surprisingly well, but can still fall apart in many real-world cases. Here's a fun example of an adversarial model:
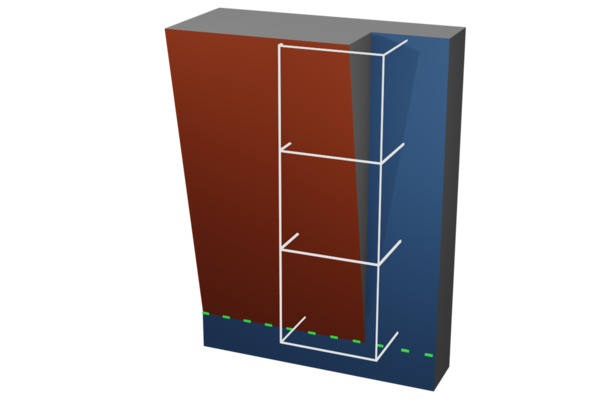
Cells are shown as white cubes in this picture. Notice that each of the three cells has intersections with both the red and blue planes. Solving the QEF is effectively asking for the location where the planes intersect, which is shown by the green dotted line at the bottom of the model.
This means that all three cells will have a vertex that wants to escape the cell and snap to the green line. This will likely lead to bad triangles and self-intersections in the mesh.
This is also a scale-invariant adversarial model: you can't necessarily escape the trap by subdividing the cells into smaller cells.
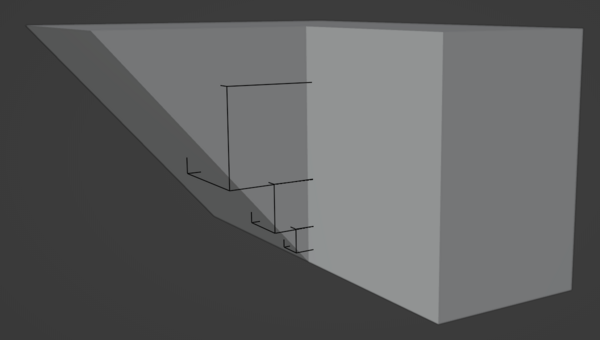
Notice that the cells are self-similar; by carefully positioning the adversarial feature, we can trigger this edge case for an arbitrarily small cell.
So, what's to be done?
One option is to give up: enforce that vertices must be constrained within their cells. This makes it easier to avoid self-intersections and other mesh deficiencies, but results in a worse-looking model:

A more robust fix would be to allow for multiple vertices per cells to improve sharp features. Manifold Dual Contouring allows more than one vertex per cell, but only to ensure manifoldness. In this case, the cell only needs a single vertex to be manifold, but wants more than one vertex to properly reproduce the sharp features.
I'm not familiar with any algorithms in the literature that do this; if you know of one, please let me know!