Matt Keeter // Graphene

About

Graphene is a tiny implementation of hierarchical dataflow programming.

If you're new to this kind of programming, think of it as a spreadsheet:

• You create cells with values or formulas inside
• These cells can refer to each other
• When one cell changes, everything that uses it changes too

Here's a graph that calculates area and circumference of a circle, given a radius r and the value of pi:

When the radius (or pi) changes, area and circumference are automatically updated.

Graphene extracts the core ideas from Antimony (some of which are described in my Dataflow Engine writeup) and implements them in under 500 lines of Racket.

Core ideas

Everything is code

For graph-based programming to be useful, it must be at least as powerful as its plain-text counterpart.

In Graphene, every datum in a graph is a full-fledged Racket script. Datums are free to define variables, helper functions, etc, and the returned value of a datum is the result of its last expression.

Dependency tracking

Every datum in a graph is evaluated in an environment that includes other datums in that graph. In this environment, other datums are no-argument functions. Calling one of these functions both returns the value and records the lookup.

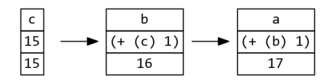
In the graph below, (+ 1 (b)) both looks up the value of b and records that a cares about b's value.

A graph stores tables that record forward, inverse, and upstream lookups.

• Forward means that one datum called another
• Inverse is the opposite of forward
• Upstream is the union of the datum itself and all forward lookup's upstream tables. This represents everything that could affect a particular datum.

This graph above has the following lookup tables:

Forward	a	b
	b	c
	c	None
Inverse	b	a
	c	b
	a	None
Upstream	a	a, b, c
	b	b, c
	c	c

With this information, we can correctly propagate changes through the graph.

Using the upstream table, the system also detects (and raises an error on) circular dependencies:

Namespaces and hierarchy

Why are hierarchical graphs useful?

• Information hiding: Implementation details shouldn't be globally visible
• Organization: It's human-friendly to group related logic into a single block

Let's walk through an example of a system with two subgraphs:

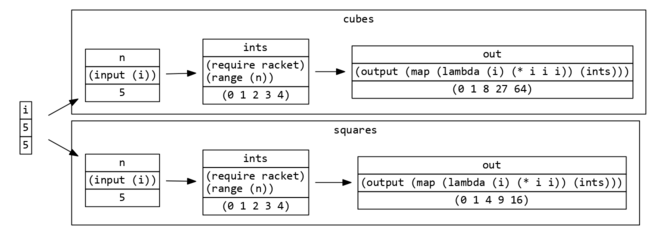
The interesting parts here are the input and output keywords:

• input indicates that a datum is evaluated in its parent graph's environment
• output makes a datum's value visible to its parent graph

How does this apply to the example above?

• The n datums in subgraphs are labelled as inputs, so they grab i from the parent environment and share it in the subgraph
• The out datums are labelled as outputs, so they are visible to the outside world
• The ints datums are implementation details, so the outside world can't see them; they could be changed with no consequences

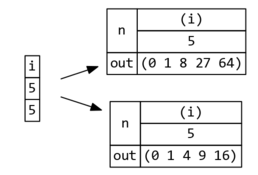
This design naturally lends itself to a user-friendly display that exposes

• Editable expression and resulting value of input datums
• Value of output datums

For the graph above, the hierarchical view looks something like this:

Change propagation

Each graph stores a dirty queue, which is a list of datums that need re-evaluation.

Updating the graph is done by popping the head off the queue, evaluating it, and inserting its children (i.e. anything that looked it up) into the queue.

Here's what that looks like in code (read topolist as queue for the moment):

(define (graph-sync! g)
  (unless (topolist-empty? (graph-dirty g))
    ;; Get the first item from the list and evaluate it
    (let* ([head (topolist-pop! (graph-dirty g))]
           [changed (graph-eval-datum! g head)])
      ;; If it changed, add all of its children to the dirty list
      (when changed
        (map (lambda (k) (graph-dirty! g k))
             (lookup-inverse->list (graph-lookup g) head)))
      ;; Recurse until the dirty list is empty
      (graph-sync! g))))

Now, what's a topolist?

Given this queue of datums that need to be re-evaluated, we should schedule them in an order that minimizes re-re-evaluation.

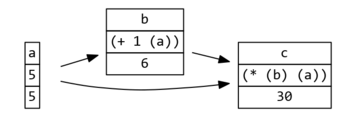
When a changes, the correct re-evaluation order is b then c;
not c, then b, then c again.

Expressed formally, we want a topologically sorted lists of datums to evaluate.

In Graphene, I define a topolist structure that creates a topologically sorted list for a given comparison operator.

When used in the graph, the comparison operator is whether a particular datum is downstream of another.

Here's what this looks like in the graph constructor:

(define (make-graph)
  (let* ([lookup (make-lookup)]
         [comp (lambda (a b) (lookup-downstream? lookup a b))]
         [dirty (make-topolist comp)])
    (graph (make-hash) lookup dirty #f)))

The implementation also includes a topolist-pops! function, which returns every item in the list until a dependency is found.

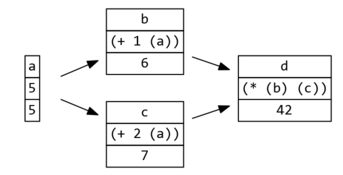
In this graph, when a changes, topolist-pops! would return '(b c).

This could enable automatic parallelization of the graph update (since b and c can be evaluated independently); implementation is left as an exercise for the reader.

Comparison to Antimony

(Feel free to skip this section if you haven't worked with Antimony's graphs;
this is very much an inside baseball discussion.)

Graphene is primarily a toy library and a way to practice my Scheme-fu. However, it does solve a few interesting problems that Antimony's graphs encounter.

Correct by construction

Graphene ensures that a graph's state is correct by construction. The data in the graph can be invalid or ill-formed, but the structure of the graph itself is guaranteed to be valid.

Consider the following graph in Antimony:

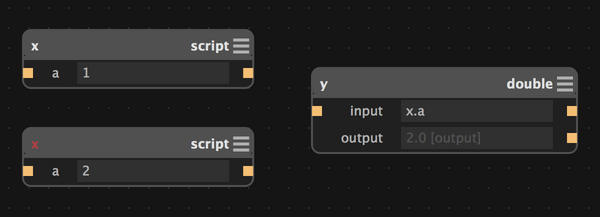
There's an ambiguity here: the graph has two top-level nodes named x. In practice, the one that was added first wins; this adds an awkward path-dependence to what should be a pure function of the graph's state.

In contrast, Graphene will raise an error if you attempt to create two datums with the same identifier.

No nodes, only subgraphs

Graphene also simplifies Antimony's subgraph / node distinction by eliminating nodes.

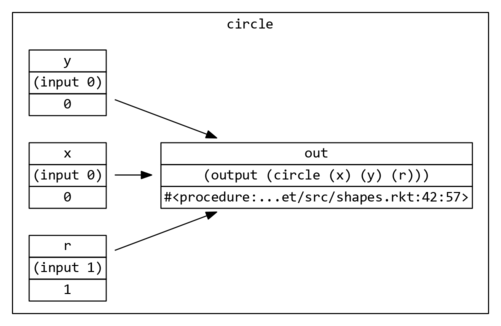
In Antimony, you could represent a circle as either a script node:

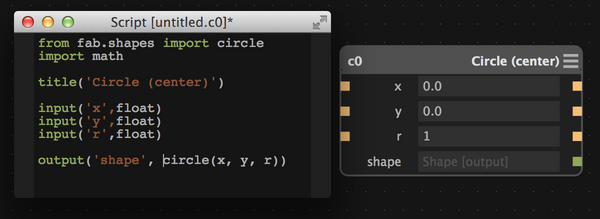
or a subgraph, which looks the same on the surface:

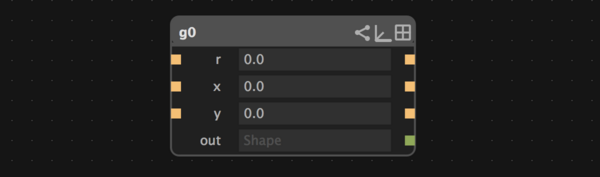
but contains a graph within itself (ad infinitum):

Graphene makes the opinionated decision that the latter is preferable, and removes nodes. To understand why, consider the two uses for nodes in Antimony:

• To contain larger chunks of code, e.g. with intermediate results
• To encapsulate multiple inputs and outputs

Since Scheme is an expression-oriented language, individual datums can define helper functions, intermediate values, etc. This answers our first use case for nodes.

With the first reason for nodes eliminated, the second isn't strong enough to justify them: subgraphs do just as well at encapsulating multiple inputs and outputs.

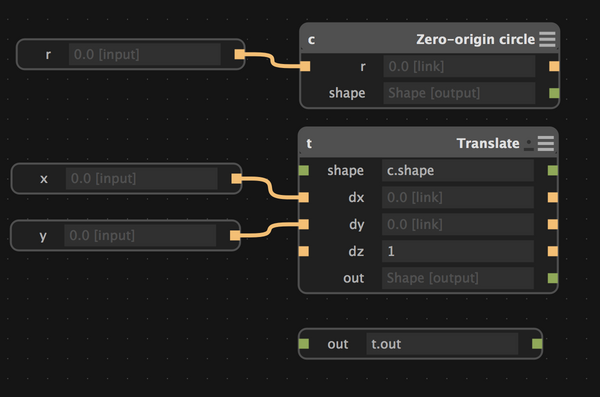
Hence, the canonical way to make the circle node in Graphene is as a subgraph:

Download

Source for Graphene is available on Github.

It is released under the GPL (version 2 or later).

         

© 2010-2024 Matthew Keeter